 О ленте Мёбиуса я уже писала, пришла очередь и бутылки Клейна. Что же это такое? Это - математическая неориентируемая поверхность, в
которой неразличимы внутренняя и внешняя стороны. Бутылка Клейна впервые была
описана в 1882 году немецким математиком Феликсом Клейном. Эта
поверхность тесно связана с другой загадочной поверхностью - лентой Мебиуса. Исходное название
бутылки Клейна - "Klein Fläche" (поверхность Клейна).
Однако, в названии слово Fläche было интерпретировано как Fla-s-che (бутылка),
и из-за доминирования английского языка утвердилось в математической науке, и
позднее термин "бутылка Клейна" также вошел в обиход и в Германии.
О ленте Мёбиуса я уже писала, пришла очередь и бутылки Клейна. Что же это такое? Это - математическая неориентируемая поверхность, в
которой неразличимы внутренняя и внешняя стороны. Бутылка Клейна впервые была
описана в 1882 году немецким математиком Феликсом Клейном. Эта
поверхность тесно связана с другой загадочной поверхностью - лентой Мебиуса. Исходное название
бутылки Клейна - "Klein Fläche" (поверхность Клейна).
Однако, в названии слово Fläche было интерпретировано как Fla-s-che (бутылка),
и из-за доминирования английского языка утвердилось в математической науке, и
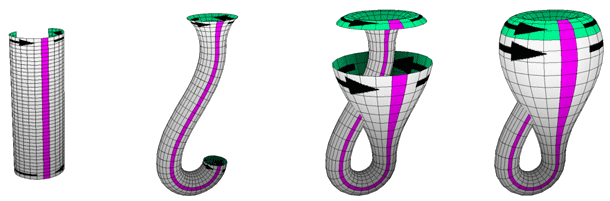
позднее термин "бутылка Клейна" также вошел в обиход и в Германии.Как же она выглядит? Представим себе бутылку с отверстием в дне. Теперь мысленно удлиним горлышко бутылки, изогнем его в обратном направлении и направим внутрь бутылки сквозь стенку, не касаясь ее (это невозможно произвести в трехмерном пространстве), далее удлиним горлышко до дна бутылки и соединим края горлышка с краями отверстия в дне бутылки. Настоящая бутылка Кляйна в четырехмерном пространстве не пересекается сама с собой. Обязательно смотрим видео!!!
В отличие от реальных бутылок, поверхность Клейна не имеет границы, где бы
она прерывалась. В отличие от шара или тора, муха, ползущая по поверхности
бутылки Клейна, может попасть с внешней стороны на внутреннюю, не проходя сквозь
поверхность.
Свойства.Если рассечь бутылку Клейна на две половинки вдоль плоскости симметрии, то получатся две зеркальных ленты Мебиуса, одна - с разворотом вполоборота вправо, другая - с разворотом вполоборота влево. Фактически, возможно рассечь бутылку Клейна так, что получится одна лента Мебиуса. Иначе, бутылка Клейна может быть представлена в виде двух лент Мебиуса, соединенных друг с другом обычной двухсторонней лентой. На рисунке ниже внутренняя поверхность этой ленты окрашена белым цветом, а внешняя - голубым.

На анимацию можно смотреть вечно!
ОтветитьУдалитьКлассное видео!
ОтветитьУдалитьЗавараживает.
ОтветитьУдалитьГде вы такие видео берете?
ОтветитьУдалитьКак интересно!
ОтветитьУдалитьДа, видео интересное.
ОтветитьУдалитьКлассная штука!
ОтветитьУдалитьУдивительно!
ОтветитьУдалить